Painted Cube or Cuboid Cutting Problems, Concept, Tricks, Technique and Shortcuts
Painted Cube Cutting
INTRODUCTION

Cubes:
A cube is a three-dimensional solid object that is bounded by six square faces, facets or sides, with three edges meeting at each vertex. It has 12 edges, 6 faces and 8 vertices.

Important Points :-
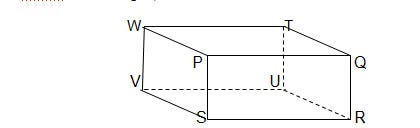
I. There are 6 faces in the cube i.e., PQRS□, TUVW□, QRUT□,PSVW□, PQTW□ and SRUV□.
II. The opposite faces are congruent and in parallel planes.
III. Vertex is a point where three edges meet each other.
IV. There are 8 corners in the cube i.e. P, Q, R, S, T, U, V & W
V. Always four faces are adjacent to one face.
VI. There are 12 edges in the cube i.e., PQ, QR, RS, PS, VS, VW, PW,TW, QT, RU, UV and TU.
VII. All 12 edges are the same length
Cube Formulas:- a
Length = breadth = height = edge = a
- Diagonal of a cube = √3 x edge
- Volume of a cube = (edge)3 Diagonal →
- Total surface area of a cube = 6 x (edge)2
Cuboids:
A cuboid is a box-shaped three-dimensional solid object that is bounded by six rectangular faces, facets or sides, with three edges meeting at each vertex.
A cuboid has 12 edges, 6 faces and 8 vertices.
Important Points :-
I. There are 6 faces in the cuboid i.e., PQRS□, TUVW□, QRUT□,PSVW□, PQTW□ and SRUV□.
II. The opposite faces are congruent and in parallel planes of rectangular shapes.
III. Vertex is a point where three edges meet each other.
IV. There are 8 corners in the cube i.e. P, Q, R, S, T, U, V & W
V. Always four faces are adjacent to one face.
VI. There are 12 edges in the cube i.e., PQ, QR, RS, PS, VS, VW, PW,TW, QT, RU, UV and TU.
VII. In a cuboid, the horizontal longer side is the length (l), and shorter horizontal side is the width (w) or breadth (b). The height (h) of a cuboid is the vertical side.
VIII. There are 4l, 4b and 4h.
Cuboid Formulas:-
All Let l = length, b = breadth & h = height.
- Volume of a cuboid = l x b x h
- Diagonal of the cuboid = ll + bb + hh =DD
- Total area of the four walls =2h( l + b )
- Whole surface of cuboid = 2( lb + bh + hI )
Cutting The Painted Cube :-
If we paint a cube of the dimension a x a x a by any one colour, and then we cut it to have a.a.a symmetric cubelets, then following is the number of cubelets with colour on different faces of it.
i. Cubelets with only one face painted =6 (a-2)2
ii. Cubelets with two faces painted =12 (a-2)
iii. Cubelets with three faces painted = 8
iv. Cubelets with no face painted = (a-2)3
So, 6 (a-2)2 + 12 (a-2)+ 8 + (a-2)(a-2)(a-2) = a.a.a
Cutting The Painted Cuboid :-
If we paint a cuboid of the dimension L x B x H by any one colour, and then we cut it to have L.B.H symmetric cubelets, then following is the number of cubelets with colour on different faces of it.
i. Only 1 face painted cubes =2[(L-2)(B-2)+ (B-2)(H-2)+(L-2)(H-2)]
ii. Cubelets with two faces painted = 4 [(L-2) + (B-2) + (H-2)]
iii. Cubelets with three faces painted = 8
iv. Cubelets with no face painted = (L-2) (B-2) (H-2)
So, L.B.H = 2[(L-2)(B-2)+ (B-2)(H-2)+(L-2)(H-2)] + 4 [(L-2) + (B-2) + (H-2)] + 8 + (L-2) (B-2) (H-2)
II EXERCISE II
Directions (Q. 1–4) : Read the passage below and solve
the questions based on it.
A large cube is dipped into a tub filled with colour. Now the cube is taken out and it was observed that all its sides are painted. This large cube is now cut into 125 small but identical cubes.
1. How many of the smaller cubes have exactly one face painted?
1) 49 2) 54 3) 64 4) 150 5) None of these
2. How many of the smaller cubes have exactly 2 faces painted?
1) 25 2) 16 3) 36 4) 60 5) None of these
3. How many of the smaller cubes have exactly 3 faces painted?
1) 4 2) 8 3) 9 4) 12 5) None of these
4. How many of the smaller cubes have no face painted all?
1) 27 2) 64 3) 8 4) 100 5) None of these
5. A cube which is painted red on the outer surface is of 2 inches height 2 inches wide and 2 inches across. If it is cut into one-
inch of equal size cubes, indicate the number of cubes which are red on two sides ?
1) 8 2) 6 3) 4 4) 2 5) None of these
6. How many cubes are there in the group?

1) 10 2) 16 3) 18 4) 20 5) None of these
Directions (Q. 7–16): Two opposite surfaces of a solid cube are painted with red colour, another two opposite surfaces with blue colour and the remaining two opposite surfaces with green colour and then it is cut into 216 small cubes of 1 cm edges.
Answer the questions given below based on this information –
7. How many cubes have their three surfaces painted with different colours?
1) 6 2) 8 3) 10 4) 12 5) None of these
8. How many cubes have their three surfaces painted?
1) 6 2) 8 3) 10 4) 12 5) None of these (1)4 (2)6
9. How many cubes have only two surfaces painted?
1) 16 2) 24 3) 36 4) 48 5) None of these
10. How many cubes have only one surface painted?
1) 88 2) 96 3) 102 4) 144 5) None of these
11. How many cubes have none of their surfaces painted?
1) 48 2) 64 3) 72 4) 81 5) None of these
12. How many cubes have only one surface painted, that too red in colour?
1) 32 2) 36 3) 81 4) 64 5) None of these
13. How many cubes have only two surfaces painted, one red and the other green in colour?
1) 12 2) 16 3) 24 4) 36 5) None of these
14. How many cubes have their 2 surfaces painted green colour?
1) 0 2) 4 3) 6 4) 8 5) None of these
15. Before dividing the solid cube, what was the length of each of its edge?
1) 4 cm 2) 5 cm 3) 6 cm 4) 8 cm 5) None of these
16. How many cubes have one of their one surface painted blue and other painted red in colour (other surfaces may or may not be coloured)
1) 12 2) 24 3) 26 4) 28 5) None of these
Directions (Q. 17–21): Study the information given below very carefully and then answer the questions based on them-
(i) A block is of length 7 cm, breadth 5 cm and height 2 cm.
(ii) Its both sides with dimensions 5 cm x 2 cm are painted blue.
(iii) Its both sides with dimensions 7 cm x 2 cm are painted green.
(iv) Its both sides with dimensions 7 cm x 5 cm are painted red.
This block is cut in such a way that it is converted into small cubes of edge of 1 cm.
17. How many cubes have all the three colours painted on them?
1) 8 2) 10 3) 12 4) 16 5) None of these
18. Find the total number of small cubes?
1) 27 2) 48 3) 64 4) 70 5) None of these
19. How many cubes have only 2 surfaces painted?
1) 20 2) 26 3) 28 4) 30 5) None of these
20. How many cubes have their two surfaces painted green?
1) 4 2) 8 3) 28 4) 56 5) None of these
21. How many cubes will have their exactly 3 sides uncoloured?
- 1) 4 2) 6 3) 8 4) 10 5) None of these
Directions (Q. 22–24): A cuboid has dimensions 12 cm * 16 cm * 10 cm. Three pairs of opposite sides of this cube are painted Red, Green and Blue. The largest surfaces have been painted Red, the smallest have been painted Blue. This cuboid is subsequently broken down into smaller cubes of side 2cm.
Answer the following questions based on the information provided.
22. How many of the smaller cubes have none of their sides painted?
1) 36 2) 64 3) 72 4) 144 5) None of these
23. How many cubes have only one surface painted?
1) 36 2) 64 3) 72 4) 144 5) None of these
24. How many have exactly 2 sides painted?
1) 36 2) 48 3) 52 4) 76 5) None of these
Directions (Q. 25–29): Some cubes equal in size have been arranged in the form of a solid block as shown in the given figure. All the faces of this solid block except the bottom one have been coloured red. Now answer the questions given below:
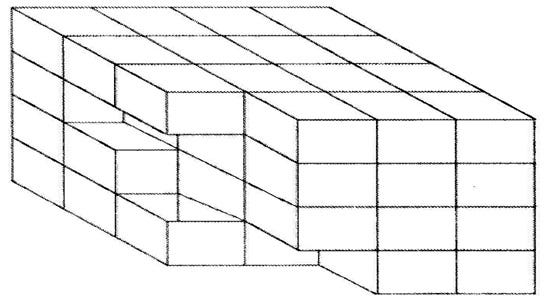
25. How many cubes are not coloured on any face?
1) 6 2) 7 3) 10 4) 11 5) None of these
26. How many cubes are coloured on one face only?
1) 24 2) 27 3) 25 4) 26 5) None of these
27. How many cubes are coloured on two faces only?
1) 13 2) 14 3) 15 4) 16 5) None of these
28. How many cubes are coloured on three faces?
1) 7 2) 8 3) 9 4) 10 5) None of these
29. How many cubes are coloured on four faces?
1) 1 2) 0 3) 2 4) 3 5) None of these
Directions (Q.30–31): How many cubes are there in the group?
30.

1 ) 80 2) 85 3) 90 4) 95 5) None of these
31.
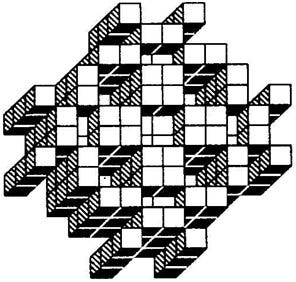
1) 138 2) 148 3) 156 4) 168 5) None of these
